为什么电容器可以给电器供电，它不是只能瞬间输出电流吗？

我们来看下图：

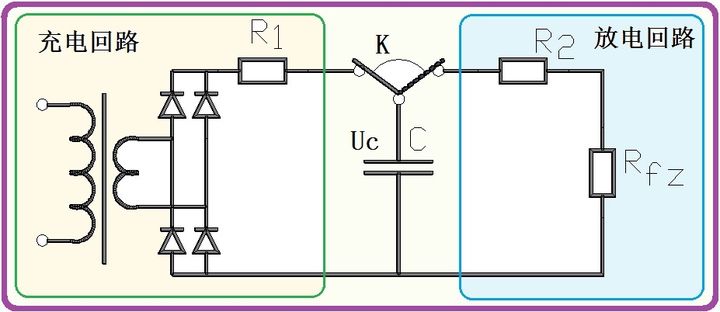
图中左侧是电容C的充电回路，图中右侧是电容C的放电回路。充电和放电的转换依靠开关K来实现。图中的R1是充电线路电阻，R2是放电的线路电阻，Rfz是负载电阻。由于题主未谈及充电回路，因此我们把它忽略掉，仅仅讨论放电回路。

我们来设想一下，现在电容上的电压已经充满，电压值为Uc。现在我们把开关K拨到右侧，也即R2的左侧。

我们看如下几件事：

第一件事：电容与电阻的乘积

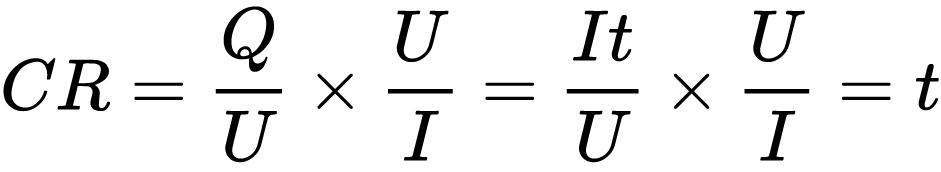
也就是说，电容与电阻的乘积是时间。

第二件事：放电回路分析

当放电时，电容相当于电源。根据基尔霍夫电压KVL定律，我们有：

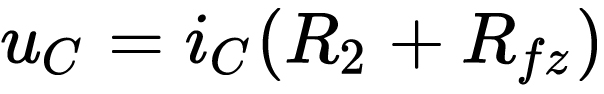
注意，这里的电容电压和电容电流均是时间的函数，电压[公式]从Uc开始逐渐减小，而电流[公式]也逐渐减小。因此电容上的电压有如下规律：

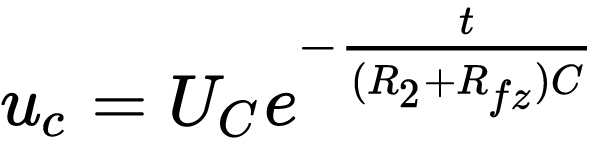
我们令

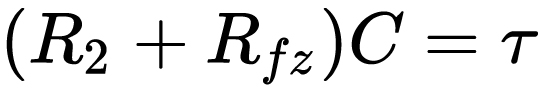
这里的[公式]又被称为时间常数，它的值等于放电回路的线路电阻R2与负载电阻Rfz之和，再乘以电容C得到的积。我们把这个式子代入到上式中，得到：

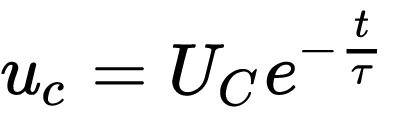
当上式中t=0时，

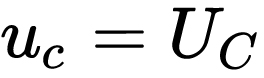
当上式中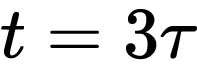时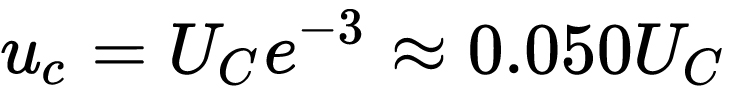，，相当于电容上的电压已经放完了。

放电曲线如下：

结论：

答案是：电容放电其实是有时间性的。在时刻0，电容上的电压为Uc，而在3倍时间常数时，电容上的电压只有5%Uc的电压了。

可见，电容放电的电压值是时间的函数。

同时，在时刻零，电流最大。随着时间的推移，电流越来越小。当时间等于5倍时间常数时，放电电流基本上等于零。